This delightful chart takes 3.4 million 4-digit PINs recovered from and disclosed in multiple data breaches

This delightful chart takes 3.4 million 4-digit PINs recovered from, and disclosed in, multiple data breaches.A 4-digit PIN can have any value between 0000 and 9999. So there are ten thousand possible Pins… and this wonderful chart contains 10,000 little squares arranged in a flat two-dimensional map having 100 rows and 100 columns. One way to think of this is that the first two digits of the Pin (00 through 99) specify one axis and the last pair of digits specify the other axis. So, every single possible PIN has its own square on this chart. And within this 3.4 million PIN dataset, the relative number of times every single possible PIN appears, sets the brightness of its square on the chart. So what do we learn from this?

 

 

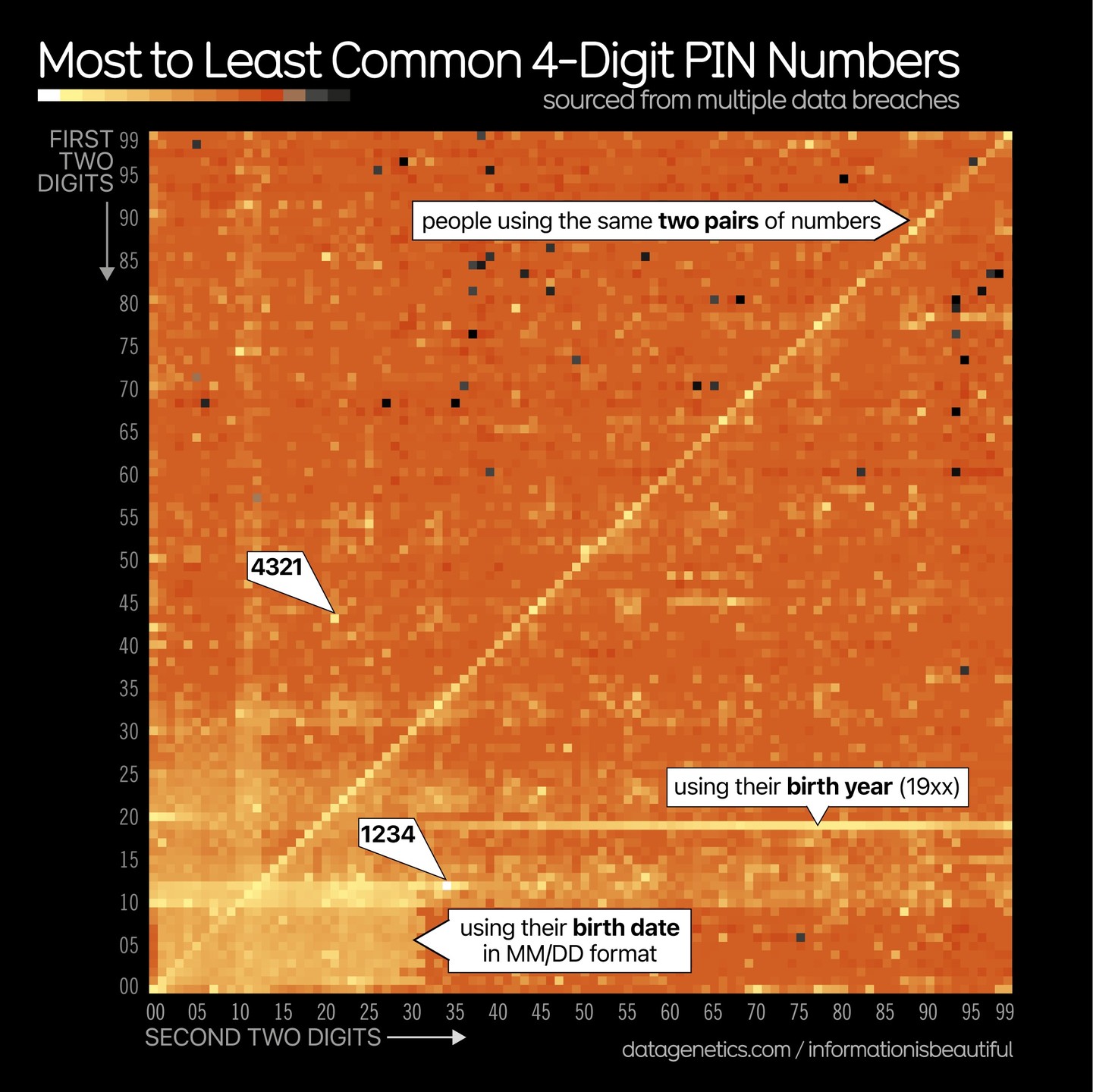
Probably the most prominent feature is a bright diagonal line running from the lower left corner of the chart, where both the first two and the last two digits are 00, to the chart’s upper right corner where the first two and last two digits are both 99. The diagonal line, then, is formed by all of the intermediate squares when their first two and last two digits are identical. This bright diagonal is telling us that a great many people chose the same pair of digits twice. But there is also some variation in the brightness along the diagonal. Human nature being what it is, the PIN6969 appears to be overrepresented relative to its neighbors.

 

 

Two other solitary bright spots would not not surprise anyone, they are the locations of the“1234” and “4321” PINs. Another prominent line is the 20th line from the bottom. Since lines arenumbered from 0, the 20th line is the line for all PINs beginning with 19. And what’s sointeresting is that the line gets gradually brighter as it moves to the right, then dims a bit towardthe end and wraps around a bit to the 20 line on the left. What’s going here? If you guessed thepeople’s birth year you would be correct. PINs often begin with 19 and they appear to bebrightest around 1980.

 

 

Another notable feature is a generally brighter region down at the lower left of the chart. Thiswould be where both the first two and the last two digits form low numbers. Why? Becausepeople used their month and day of birth with month running from 1 to 12 and day of month 1through 31. There’s a brighter horizontal stopping at 12 than the vertical stopping at 12. Thisindicates that most people chose the ordering with the month first and the day of month second.Stepping back from it and looking at the overall illumination, there’s a top to bottom brightnessvariation, but less of a left to right. So people are generally choosing 4-digit PINs with smallerfirst two digits but more randomly distributed last two.

 

 

And the final really interesting observation is that whereas most of the chart shows varyingshades of illumination, there are around 40 cells that are black or nearly black. In other words,out of all 10,000 possible 4-digit PINs, there are around 40 of those that are significantlyunderrepresented. For some reason, for example, very few people have chosen 6806. So, ifyou’re looking for a lesser chosen 4-digit PIN, there you go.

 

 

And as for the extremely low-entropy skewing observed in this dataset, get this: Just the 20 topmost used PINs (out of those possible 10,000) account for 27% of all PINs observed in use.Those top 20 are: 1234 0000 7777 2000 2222 9999 5555 1122 8888 2001 1111 12121004 4444 6969 3333 6666 1313 4321 1010. I also had the bottom 20, but they wereabsolutely uninteresting since, not surprisingly, they all just looked like random numbers.